PROIECT ANALIZA ALGORITMILOR

PROIECT ANALIZA ALGORITMILOR - ALGORITMI PENTRU DRUMURI MINIME MULTIPUNCT-MULTIPUNCT

ANALIZA PROGRAMULUI

Programul prezinta doi algoritmi pentru gasirea drumurilor minime intre toate perechile de noduri dintr-un graf orientat (algoritmi multipunct). Cei doi algoritmi care pot fi aplicati grafurilor sunt Floyd-Warshall si Johnson. Aplicatia care prezinta cei doi algoritmi a fost realizata in limbajul Java si este structurata in mai multe clase fiecare indeplinind o anumita functie. Programul ofera utilizatorului posibilitatea sa construiasca un graf orientat si sa-i aplice unul dintre cei doi algoritmi. Acest proiect a fost realizat sub forma unui applet pentru a putea fi rulat pe o pagina de internet, dar totodata poate fi compilat si rulat pe un calculator ca o fereastra independenta de browserul web. In continuare voi prezenta clasele programului si rolul pe care acestea il au:

class Proiect: este clasa principala a proiectului care contine functia main(). In interiorul ei sunt create instante ale celorlalte clase ale programului;
class Info: contine un obiect de tip InfoDoc;
class InfoDoc: reprezinta o zona text (JtextArea) in care sunt oferite unele indicatii utilizatorului in scopul de a-l ajuta sa construiasca un graf si sa vizualizeze efectele aplicarii unui algoritm;
class Optiuni: reprezinta bara de optiuni formata din mai multe butoane, fiecare cu o anumita functie;
class Suprafata: defineste zona pe care se deseneaza graful si pe care pot fi vizualizate rezultatele;
class PriorityQueue: este o clasa folosita de catre algoritmul Dijkstra si defineste o coada cu prioritati sub forma unui heap minim.

Majoritatea functiilor folosite, inclusiv cele pentru implementarea algoritmilor se gasesc in clasa Suprafata. Mai jos sunt niste snap-shoturi din timpul rularii programului.

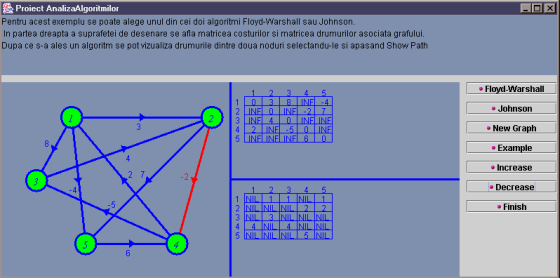
In scopul usurarii prezentarii am adaugat si un exemplu gata construit pe care se poate vedea foarte bine cum functioneaza algoritmii utilizati.

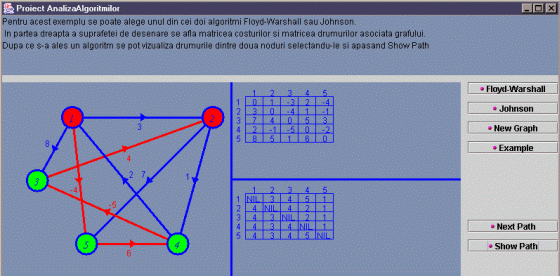
In partea dreapta fereastra principala are mai multe butoane:

Floyd-Warshall si Johnson: aplica cei doi algoritmi grafului desenat
New Graph si Example:posibilitatea de a construi un nou graf (tot ce exista inainte e sters) sau un exemplu
Increase,Decrease si Finish:daca s-a selectat o muchie, i se poate mari sau micsora costul, dupa care se apasa Finish
Next Pathsi Show Path:dupa ce s-au selectat doua noduri se apasa Show Path iar daca se doreste vizualizarea altui drum optim se da click pe Next Path

ANALIZA ALGORITMILOR

Problema drumurilor optime dintre varfurile unui graf poate fi rezolvata ruland un algoritm punct-multipunct de | V| ori pentru fiecare varf, unde V reprezinta numarul de varfuri ale grafului. Daca toate costurile muchiilor din graf au valori pozitive putem folosi Dijkstra. Daca algoritmul Dijkstra e implementat cu o coada cu prioritate sub forma unui vector atunci complexitatea va fi O(V3+VE)=O(V3).Daca este implementat cu heap-uri binare atunci complexitatea scade la O(VElgV) ceea ce reprezinta o imbunatatire pentru grafurile rare. Ca o alternativa se poate implementa coada cu prioritati folosind un heap Fibonacci care coboara complexitatea la O(V2lgV + VE). Daca graful are muchii cu cost negativ atunci Dijkstra nu mai poate fi folosit si se utilizeaza Bellman-Ford cate odata pentru fiecare nod. Complexitatea rezultata este O(V2E) ceea ce pentru un graf dens inseamna O(V4) (folosind Johnson putem obtine o complexitate mai mica).

FLOYD - WARSHALL

Algoritmul Floyd-Warshall rezolva problema drumurilor optime multipunct-multipunct intr-un graf. Nu se inpun restrictii ale arcelor, ci doar a structurii grafului. Graful nu trebuie sa contina cicluri cu cost negativ. Algoritmul este in categoria algoritmilor de programare dinamica. Solutiile problmei sunt construite recursiv asambland solutii ale unor probleme similere, dar de dimensiuni mai mici. Scris in pseudocod algoritmul Floyd-Warshall arata astfel:


Floyd-Warshall(G){
n = numar_noduri(G);
	for(i=1; i=n; i++)
	for(j=1; j=n; j++) {
		d(i,j)= w(i,j);
		if(w(i,j)=8) p(i,j)= null; else p(i,j)= i;
		}
	for(k=1; k=n; k++)
		for(i=1; i=n; i++)
			for(j=1; j=n; j++)
			if(d(i,k)+d(k,j)< d(i,j)){
			d(i,j) = d(i,k)+d(k,j); p(i,j)= p(k,j);}
			}

Daca presupunem ca graful e reprezentat printr-o matrice de adiacenta complexitatea algoritmului este O(n3). La terminarea algoritmului d(i,j) reprezinta costul drumului optim dintre i si j, iar p contine informatia cu care se poate construi acest drum optim. Acest algoritm este foarte folositor pentru grafuri medii ca marime. Codul sursa pentru functia care implementeaza acest algoritm este prezentat mai jos:

		
public void FloydWarshall() {
	fw = true;
	int suma = 0;
	   if (BellmanFord(0) == 0) parent.info.infodoc.showLine("string4");
		
for( int k = 0; k < nr_puncte; k++ )
		for( int i = 0; i < nr_puncte; i++ )
			for( int j = 0; j < nr_puncte; j++ ) {
			if (DC[i][k] == 999 || DC[k][j] == 999) suma = 999;
			else suma = DC[i][k] + DC[k][j];
			if( DC[i][j] > suma ) {
				DC[i][j] = DC[i][k] + DC[k][j];
				Pi[i][j] = Pi[k][j];
					}
				}
}

JOHNSON

Este un algoritm util in cazul grafurilor rare si este asimptotic mai bun decat Floyd-Warshall in cazul acestor grafuri. Algoritmul fie intoarce o matrice a drumurilor optime, fie avertizeaza ca in graf exista cel putin un ciclu cu cost negativ. Johnson foloseste ca subrutine Dijkstra si Bellman-Ford. Algoritmul foloseste tehnica recalcularii costurilor drumurilor dintre nodurile grafului folosind algoritmul Dijkstra pentru fiecare nod. In cazul in care se folosesc heap-uri binare complexitatea este O(VElgV). Daca graful are muchii negative algoritmul calculeaza un nou set de muchii nenegative care ne permit sa aplicam aceeasi metoda. Noul set de muchii trebuie sa indeplineasca urmatoarele conditii: - pentru oricare perechi de varfiri u,v un drum optim de la u la v este egal cu un drum optim si de la v la u folosind noile costuri; - pentru oricare muchie (u,v) costul e nenegativ; Procesarea matricei de adiacenta pentru a obtine noile costuri poate fi realizata in O(VE). Pentru a calcula noile costuri se adauga grafului inca un nod care are legaturi cu toate celelalte noduri (prin muchii de lungime 0). Ca acest nod sa poata fi adaugat ne trebuie o noua matrice cu un rang mai mare. Ruland Bellman-Ford pentru acest nod se obtin niste drumuri optime, retinute in vectorul h, care vor fi folosite la crearea noilor costuri. Codul sursa pentru acest algoritm este dat mai jos:


public void Johnson() {
		johnson = true;  	
	  for(int i=0;i < nr_puncte + 1;i++) {
		for(int j=0;j < nr_puncte+1;j++)
			if (i==0) G[i][j] = 0;
			else  if (j==0) G[i][j] = 999;		//se calculeaza noua matrice G 
				 else G[i][j] = D[i-1][j-1];      // pe baza celei initiale
			}

		
	   calcLaturi();      // functia care enumera laturile grafului (nod1,nod2)
	   //se ruleaza Bellman-Ford
   if (BellmanFord(0,G)==0) parent.info.infodoc.showLine("string4");
	   else  for(int i=0;i < nr_puncte+1;i++)
				h[i]=d[i];

	    //se calculeaza noile costuri	
	    for(int i=0;i < nr_laturi;i++) {
	   G[e[i][0]][e[i][1]] = G[e[i][0]][e[i][1]] + h[e[i][0]] - h[e[i][1]];
	   if (e[i][0]!=0 && e[i][1]!=0) DC[e[i][0]-1][e[i][1]-1] = G[e[i][0]][e[i][1]];
	   }
	  //ruleaza Dijkstra pentru toate nodurile
		for(int i=0;i < nr_puncte;i++) {
			Dijkstra(i);
			for(int j=0;j < nr_puncte;j++) {
				if (t[j]== -1) Pi[i][j] = t[j];
				else if (i!=j ) Pi[i][j] = t[j]+1;
						else  Pi[i][j] = t[i];
				int suma = 0;
				if (d[j] == 999 || h[j+1] == 999 || h[i+1] == 999) suma =999;
				else suma = d[j] +h[j+1] - h[i+1];
				matback[i][j] = suma;
				 }
			}
	 	for(int i=0;i < nr_puncte;i++) {
	 		for(int j=0; j < nr_puncte;j++)
	 		DC[i][j] = matback[i][j];
	 		}
	 }

DIJKSTRA SI BELLMAN-FORD

Acestia rezolva problema drumurilor de cost minim punct-multipunct. Ambii folosesc urmatoarele doua functii:


init_graf(G,s){
V = noduri(G);
for-each(u.V) {d(u)=8; p(u)=null;}
d(s)=0;
}

relaxare_arc(u,v){
if(d(v)>d(u)+w(u,v)) {d(v)=d(u)+w(u,v); p(v)=u;}
}

void Dijkstra(int source) {
	int minKey = 0;
	int u = 0;

	initialize(source);
	int x = nr_puncte+1;
	PriorityQueue Q = new PriorityQueue(x,d);


	while(Q.heapSize() > 0) {
	 minKey = Q.getMin();
	 u = Q.extractMin();
		d[u] = minKey;
		s[u] = 1;
		for(int j=1;j <= Q.heapSize();j++)  relax1(Q,u,j);
		Q.makeHeap();	
		}	
		
	}
int BellmanFord(int source) {
		initialize(source);    
		for(int i=0;i < nr_puncte+1;i++)         
			for(int j=0;j < nr_laturi;j++)  
				relax(e[j][0],e[j][1]);
		for(int i=0;i < nr_laturi;i++)
			if(d[e[i][1]] > d[e[i][0]]+G[e[i][0]][e[i][1]]) return 0;
   		return 1;
   }

Algoritmul Dijkstra lucreaza pentru costuri pozitive ale arcelor grafului . Dijkstra poate fi rescris în scopul determinarii eficiente a nodului cu d(u) minim, eliminat din V în fiecare etapa a algoritmului. În acest caz, multimea V poate fi organizata ca heap minimizant în raport cu proprietatea d a nodurilor. Folosind notatiile n = card(V) si m = card(E), complexitatea algoritmului de mai sus este