Aceasta este pagina de proiect Analiza Algoritmilor
This site is dedicated to the Algorithm Analisis project:
http://www.gavieritei.home.ro
Daniel George Avieritei
334 CA
Computer Science Engineering
Politehnical Institute of Bucharest
Documentatia aici.
Exemple aici.
Sursele aici.
Bibliografia aici.
Ex Codul Sursa aici
Teoria grafurilor
Aşa cum putem abstractiza harta străzilor folosind un graf orientat pentru a găsi cel mai scurt drum între două noduri, putem de asemenea să interpretăm un graf orientat ca pe o “reţea de transport” şi să-l folosim pentru a răspunde unor întrebări despre transportul de material. Sa ne imaginam traseul materialului printr-un sistem de la o sursă, unde este produs, la o destinaţie, unde este consumat. Sursa produce materialul într-un anumit ritm şi destinaţia îl consumă în acelaşi ritm. Transportul de material în oricare punct din sistem este, intuitiv, ritmul în care materialul se mişcă. Reţelele de transport pot fi folosite ca model teoretic pentru reţelele de conducte, părţi ale liniilor de asamblare, curentul care circulă prin reţelele electrice, informaţia care circulă prin reţelele de comunicaţie.
Fiecare arc dintr-o
reţea poate fi imaginat ca o conductă prin care circulă
material. Fiecare conductă are o capacitate specificată, care
reprezintă “ritmul” maxim la care materialul poate circula prin
conductă, ca de exemplu 2000 metri cubi de lichid pe oră printr-o
conductă, sau curent electric de 20 amperi care poate trece printr-un
conductor.
O reţea de transport G=(V,E), cu sursa s şi destinaţia t, este un graf orientat în care fiecare muchie (u,v) Î E are o capacitate pozitivă c(u,v) ł0. Dacă (u,v) Ď E, vom considera c(u,v)=0.
Nodurile dintr-o reţea, în afară de s şi t, sunt doar punctele de intersecţie ale conductelor: materialul trece prin ele fără a fi colectat. Adică ritmul în care materialul intră într-un nod trebuie să fie egal cu ritmul în care materialul iese din nod. Aceasta este proprietatea de conservare a fluxului şi este aceeaşi ca şi legea lui Kirchhoff pentru cazul în care “materialul” este curentul electric (“flux“ este echivalent cu “ritm”, semnificând o anumită cantitate într-o anumită perioadă de timp).
Un flux în G este o funcţie f:VxV®R care are următoarele proprietăţi:
·
0 Ł fi,j Ł ci,j , adică fluxul transportat pe
orice arc trebuie să fie nenegativ şi subcapacitar;
- SjÎV fj,i = SjÎV fi,j , " iÎV-{s,t}, adică conservarea fluxului.
Dacă f este un flux în reţeaua G=(V,E), atunci se numeşte valoarea fluxului f numărul:
v(f) = SjÎV fj,t - SjÎV ft,j
V(f) poate fi interpretat ca fiind fluxul net care ajunge în ieşirea reţelei sau fluxul net care intră în reţea prin s.
Problema
fluxului maxim
Se dă reţeaua G=(V,E) cu sursa s şi destinaţia t, şi funcţia capacitară c. Se cere să se determine un flux de valoare maximă.

Fie P un drum oarecare în graful suport
al lui G (acelaşi graf în care se
ignoră sensurile arcelor), şi e=vivj o muchie a lui P; dacă e corespunde arcului vivj al lui G, e se numeşte arc direct al drumului P; dacă e corespunde arcului vjvi al lui G, atunci e se numeşte arc invers.
De exemplu, în graful de mai sus, să considerăm că drumul P trece prin nodurile 1,2,4,5,6,7. Fiecare din muchiile (1,2), (2,4), (4,5) şi (6,7) sunt arce directe ale drumului P pentru că au acelaşi sens de parcurgere ca şi cel din reţea; în schimb muchia (5,6) a drumului P este un arc invers.
Fie P un drum şi vivj o muche din P. Se numeşte capacitatea reziduală a lui vivj numărul:
r(ij) = ci,j – fi,j dacă vivj este arc direct în P
fj,i dacă vivj este arc invers în P
În exemplul de mai sus, primul număr de pe arc reprezintă capacitatea arcului, iar cel de-al doilea, fluxul. Astfel, capacitatea reziduală a arcului (4,5), r(4,5) va fi egală cu c4,5 – f4,5 = 8 – 3 = 5. Pentru arcul (5,6) vom avea:
r(5,6) = f6,5 = 4.
Capacitatea reziduală a drumului P se notează cu r(P) şi este egală cu minimul dintre capacităţile reziduale ale muchiilor din P:
r(P) = min eÎP r(e)
Fie P={4,5,6}. Cum r(4,5)=5 şi r(5,6)=4 rezultă că r(P)=4.
Se numeşte drum de creştere a fluxului f în reţeaua G, un drum de la s la t care are capacitatea reziduală mai mare ca zero.
În exemplul nostru, să luăm drumul 1,2,4,3,6,7 şi să vedem dacă este un drum de creştere: avem r(1,2)=8, r(2,4)=1, r(4,3)=5, r(3,6)=3 şi r(6,7)=6, deci capacitatea reziduală a drumului este 1; rezultă că drumul nostru este un drum de creştere.
Teorema 1: Un flux f este de valoare maximă într-o reţea G, dacă şi numai dacă, nu există drumuri de creştere a fluxului f în reţeaua G.
Teorema 2: Dacă toate capacităţile sunt întregi, atunci există un flux de valoare maximă cu toate componentele întregi.
Aceste două teoreme stau la baza algoritmului Ford-Fulkerson pentru determinarea unui flux de valoare maximă.
Primul pas al algoritmului constă în determinarea unui flux iniţial admisibil, adică fixarea valorilor lui f pentru fiecare arc astfel încât să se respecte proprietăţile fluxului (cele din definiţie). Un astfel de flux admisibil este şi cel care are flux 0 pe fiecare arc. Se verifică uşor că cele două proprietăţi sunt respectate: fluxul este subcapacitar pe orice arc, iar conservarea fluxului este evidentă: în fiecare nod intră 0 unităţi şi ies de asemenea 0.
La pasul doi se va determina un drum de creştere P. Acesta se poate găsi printr-o simplă parcurgere în adâncime, mergând întotdeauna doar pe arcele care au capacitatea reziduală mai mare ca zero. Pornind de la fluxul anterior şi folosind drumul de creştere găsit se va obţine un nou flux, f1 de valoare mai mare decât f, astfel: fie r(P) capacitatea reziduală a drumului găsit; pentru fiecare arc direct din P se va mări fluxul cu r(P), iar pentru arcele inverse fluxul va fi scăzut tot cu r(P). Să dăm un exemplu: pentru drumul de creştere 1,2,4,5,6,7, avem r(P)=1; deci noile valori ale fluxului vor fi: f1,2=3+1=4, f2,4=3+1=4, f4,5=3+1=4, f5,6=4-1=3 şi f6,7=0+1=1.
Faptul că r(P) este egal cu minimul dintre capacităţile reziduale ale arcelor din P, ne asigură că pentru orice e=(u,v) Î P, avem r(e) ł r(P), adică pentru arcele directe se mai poate adăuga r(P) flux fără a depăşi capacitatea arcului, iar pentru arcele inverse se poate scădea r(P) fără a obţine un flux negativ. Deci noul flux f1 va respecta prima proprietate a fluxului; să vedem dacă va respecta şi conservarea fluxului.
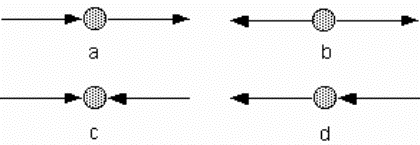
Deoarece arcele pot fi de
două tipuri, vom întâlni patru cazuri, ca în figură (sensul de
parcurgere este de la stânga la dreapta):
a) ambele arce sunt arce directe, deci fluxul va creşte pe ambele cu aceeaşi cantitate r(P); dacă egalitatea din legea conservării fluxului era verificată, va fi de asemenea verificată şi după modificarea fluxului: practic vom adăuga aceeaşi cantitate ambilor termeni;
b) primul arc este invers,
iar cel de-al doilea este direct, deci pe primul arc fluxul va scădea, iar
pe al doilea va creşte; deoarece ambele arce “ies” din nod, iar fluxul de
pe unul creşte, iar de pe celălalt scade cu aceeaşi cantitate,
rezultă că suma a tot ce “iese” din nod va rămâne constantă
şi deci fluxul se va conserva;
c) analog cu b);
d) ambele arce sunt
inverse; de această dată se va scădea aceeaşi cantitate din
ambii termeni ai egalităţii conservării fluxului, deci
egalitatea se va păstra.
Acest pas se va repeta
atâta timp cât exista un drum de creştere; în final, conform teoremei 1,
fluxul găsit va fi maxim.
Finalitatea algoritmului
este asigurată de faptul că la fiecare iteraţie valoarea
fluxului creşte cu o cantitate mai mare decât zero; cum valoarea fluxului
maxim este finită rezultă că este necesar un număr finit de
iteraţii ale pasului 2.
Se consideră că sursa reţelei este nodul 1, iar destinaţia este nodul n.
Calculul complexitatii aici
Modulul de intrare:
Appletul initial arata asa:
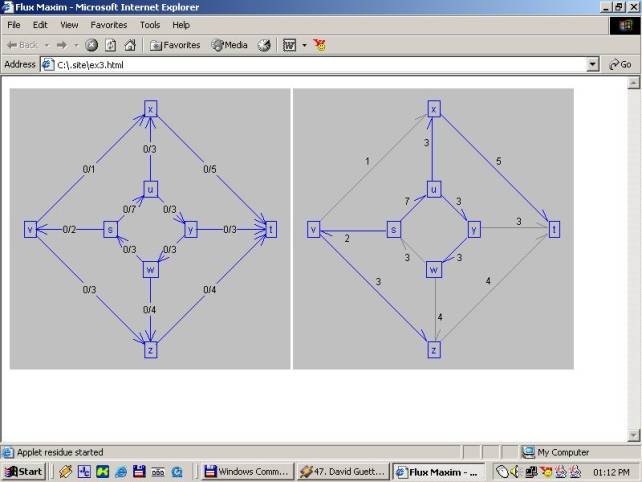
Etape ale algoritmului vazute la lucru, la fiecare click de mouse algoritmul inainteaza:
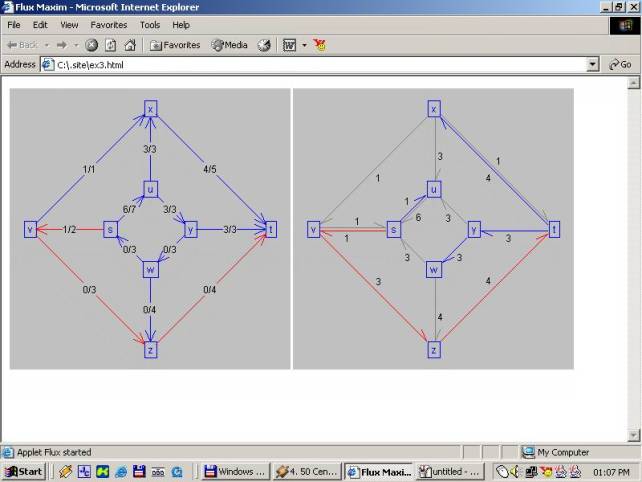
Se observa culoarea muchiilor.
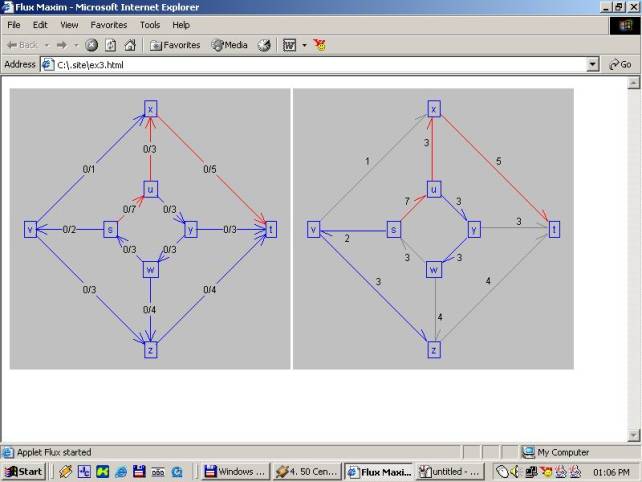
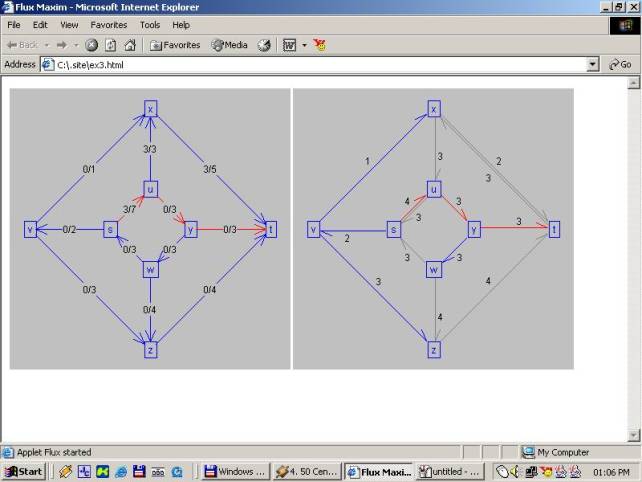
Catre pagina de lucru aici
Ford-Fulkerson(G,s,t)
1: pentru fiecare arc (u,v) ce apartine E[G] executa
2: f[u,v]=0
3: f[v,u]=0
4: cat timp exista un drum p de la s l at in reteaua reziduaal Gf executa
5: cf{p}=min {cf(u,v): (u,v) este pe drumul p}
6: pentru fiecare arc (u,v) din p executa
7: f[u,v]=f[u,v]+cf(p)
8: f[v,u]= -f[v,u]
Timpul de executie a algoritmului Ford-Fulkerson depinde de modul de determinare (in linia 4) a drumului de ameliorare p.Daca drumul este ales intr-un mod nepotrivit, se poate ca algoritmul sa nu se opreasca; valoarea fluxului creste succesiv, dar nu converege catre valoarea maxima. Daca drumul de ameliorare se alege folosind un algoritm de cautare in latime atunci timpul de executie al algoritmului este polinomial.
In practica problemele de flux maxim apar de obicei cu capacitati care sunt numere intregi.O implementare directa a algoritmului Ford-Fulkerson are un timp de executie O(E|f*|), unde f* este fluxul maxim obtinut de algoritm. Timpul de executie al liniilor 1-3 este Ф(E). Ciclul cat timp din liniile 4-8 este executat de cel mult |f*| ori, deoarece valoarea fluxului la fiecare pas cu cel putin o unitate.
Ciclul cat timp poate fi executat eficient daca structura de date folosita la implemetarea retelei G=(V,E) se gestioneaza eficient. Sa presupunem ca pastram o structura de date corespunzatoare unui graf orientat G’=(V,E’), unde E’={(u,v): (u,v) apartine E sau (v,u) apartine lui E}. Arcele din g sunt si arce in G’, deci este usor sa se gestioneze capacitatile si fluxurile intr-o astfel de structura. Dandu-se un flux f in g, arcele din reteaua reziduala Gf costau din toate arcele (u,v) din G’ pentru care c(u,v)-f[u,v]<>0. timpul de gasire a unui drum in reteaua reziduala este deci O(E’)=O(E), indiferent daca folosim cautare in adancime sau in latime. Fiecare iteratie a ciclului cat timp se executa in O(E) unitati de timp, timpul total de executie a algoritmului Ford-Fulkerson este deci O(E|f*|).E se refera de fapt la numarul de muchii din retea.
public boolean mouseDown(Event event, int i,
int j){
if(pas == 1){
pas1();
if(v[tnode].dist < 0){pas = 0;}
else{pas = 2;}}
else if(pas == 2){pas2();pas = 1;}
else{pas0();pas = 1;}
repaint();
return true;}
void
refacDrum(){/*reface fluxurile pe drumul de ameliorare deja selectat*/
for(int i = 0; i < n; i++){
v[i].delta_plus = v[i].delta_minus
= -1; }
for(int j = 0; j < m; j++){
e[j].delta_plus = e[j].delta_minus
= -1; }
for(int k = 0; k < m; k++){
int l = e[k].nod_plus;
if(v[l].delta_plus == -1){
v[l].delta_plus = k; }
else{
for(l = v[l].delta_plus;
e[l].delta_plus >= 0; l = e[l].delta_plus) { }
e[l].delta_plus = k;}
l = e[k].nod_minus;
if(v[l].delta_minus == -1) {
v[l].delta_minus = k;}
else{
for(l = v[l].delta_minus;
e[l].delta_minus >= 0; l = e[l].delta_minus) { }
e[l].delta_minus = k;}}}
void stCale(){/*determina calea de la
s(sursa) la t(destinatie), determinand capacitatile reziduale si minimul
acestora*/
int ai[] = new int[100];
for(int k = 0; k < n; k++){
v[k].prev = v[k].dist = -1;
v[k].l = 0;}
for(int l = 0; l < m; l++){
e[l].st = -1;}
int j;
int i = j = 0;
boolean flag = false;
ai[i] = snode;
v[snode].dist = 0;
int l1 = v[snode].delta_plus;
int i1 = 0;
for(; l1 >= 0; l1 =
e[l1].delta_plus){
if(i1 < e[l1].capacitate){
i1 = e[l1].capacitate;}}
v[snode].l = i1;
for(; j <= i; j++){
int k2 = v[ai[j]].dist;
for(int i2 = v[ai[j]].delta_plus;
i2 >= 0; i2 = e[i2].delta_plus){
if(e[i2].capacitate -
e[i2].flux != 0){
int j1 = e[i2].nod_minus;
if(v[j1].dist < 0){
v[j1].dist = k2 + 1;
v[j1].prev = ai[j];
v[j1].p_muchie = i2;
v[j1].l =
Math.min(v[ai[j]].l, e[i2].capacitate - e[i2].flux);
e[i2].st++;
ai[++i] = j1;}}}
for(int j2 = v[ai[j]].delta_minus;
j2 >= 0; j2 = e[j2].delta_minus){
if(e[j2].flux != 0){
int k1 = e[j2].nod_plus;
if(v[k1].dist < 0){
v[k1].dist = k2 + 1;
v[k1].prev = ai[j];
v[k1].p_muchie = j2;
v[k1].l =
Math.min(v[ai[j]].l, e[j2].flux);
e[j2].st++;
ai[++i] = k1;}}}}}
void pas0(){
for(int i = 0; i < m; i++){
e[i].flux = 0;}
stCale();}
void pas1(){
if(v[tnode].dist < 0){return;}
for(int i = tnode; v[i].prev >= 0;
i = v[i].prev){
e[v[i].p_muchie].st++;}}
void pas2(){
int l = v[tnode].l;
int j;
for(int i = tnode; (j = v[i].prev)
>= 0; i = j){
int k = v[i].p_muchie;
if(e[k].nod_minus == i){
e[k].flux += l;}
else if(e[k].nod_plus ==
i){
e[k].flux -= l;}}
stCale();}
Bibliografia acestui proiect:
- "Introducere in Algorimi" de Thomas Cormen (Editor), Charles E. Leiserson, Ronald L. Rivest, 1990, Massachusetts Institute of Ttechnology Press.
- “Aplicatii C/C++” Stoilescu Dorian, Editura Radial, editia 1998
- “Algoritms” by Robert Sedgewick, Brown University.